NY Times Fudges the Numbers again

As a daily "commuting" cyclist and having just returned from a 270-mile bike ride, I am aware of the dangers of riding in the roads.  However, I still feel the need to call out the NY Times when they use a poor analysis to show safety has declined.

Today's NY Times featured an article on increasing vehicle deaths with the following explanation and chart: "...more people have been traveling by bike and motorcycle in the U.S. Cycling advocates said they expected there would be safety in numbers as more people biked and drivers grew accustomed to sharing the road, reducing deaths. Instead, the opposite has happened."

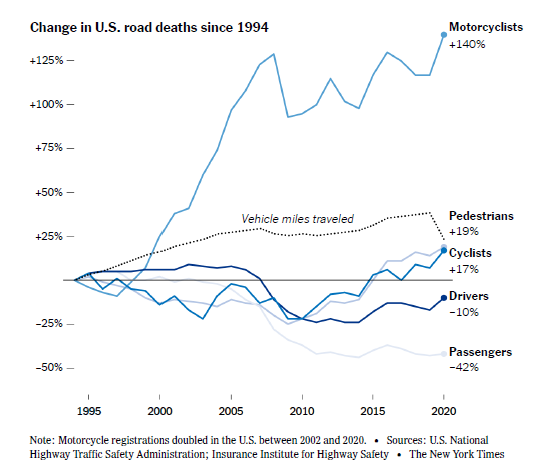
Comparing the raw changes in deaths is a 'rookie' error in statistical analysis.  With a growing population, and, as the article acknowledges, a growing number of cyclists and motorcycle riders, we can only understand whether the roads got safer by comparing fatality rates.  For vehicle accidents, usually miles driven is used.  For motorcycles and cyclists, where those figures are not easily estimated, we could at least use number of cyclists/motorcyclists.  But the NY Times completely ignores rates, thereby invalidating the analysis completely.

To see how ignoring the rates can change things, let's consider motorcycle deaths.  Instead of taking raw deaths, which increased 140%, let's use the death rate.  The only evidence the NY Times provides regarding the number of motorcyclists is at the bottom of the chart, where we see a note that says motorcycle registration doubled from 2002 to 2020.  

The chart doesn't show the exact number of deaths per year, but we can see they increased 140% for motorcyclists between 1995 and 2020.  In 2002, it appears to have increased about 50%, and certainly more than 25%.  So let's say deaths were at 1000 in 1995.  In 2002, they were around 1500, but definitely more than 1250.  In 2020, they would be at 140% more than 1000, or 2400.  So deaths increased about by 2400/1500-1, or 60% since 2002, and at most by 92%.  But motorcycle registration doubled, as the note at the bottom of the chart says.  So deaths per registered motorcycle decreased between 2002 and 2020 (the only period where we have data to calculate the rate), perhaps quite substantially.  

To figure this out suppose the number of motorcycles registered in 2002 was 4 million (which is supported by this article), making the number 8 million in 2020.  The death rate in 2002 would then be about 1500/4 million, or 375 per million motorcycles in 2002, or, using the lower number of deaths, 1250/4 million, which is 312.5 per million motorcycles.

In 2020 it would be 2400/8 million, which is 300 deaths per million motorcycles.

So the death rate declined, by about 20% ((375-300/375) and by at least 4% (312.5-300)/312.5.

Note that the exact number of deaths in 1995 or motorcycles in 2002 does not change the conclusion regarding percentage changes at all.  You could say 1995 had X deaths and 2002 had Y motorcycles.  Once you apply the same math of increasing the death and motorcycle rate, the overall death rate still declines by the same percentages. So the NY Times conclusion regarding motorcyclists is clearly wrong using the only data they have provided.

For cyclists, there is no note regarding the increase in cycling, so we cannot go through the same mathematical evaluation, but we know, as even the preceding quote  acknowledges, that cycling has increased substantially since 1995.  If it has increased more than the 17% that deaths have increased, then cycling too has become safer since 1995 (according to one survey, bike commuting increased 60% since 2000, but it's not clear how recreational cycling has changed).  Whatever the exact change in cycling, the NY Times is wrong to conclude an increase of 17% in deaths over 25 years means cycling has become more dangerous.  Only by accounting for the change in the number of cyclists (or miles ridden), can we determine if cycling has become more or less dangerous.

 What's the net-net?  I'm all for changes that make the roads safer, especially for cycling and pedestrians, but when you put forth such an argument, don't do it with a spurious analysis!