The Vaccines: What do the Numbers Tell Us?

I'm sure you know by now that the FDA approved the Pfizer and Moderna vaccines for emergency use.

The FDA publicly posts their applications, so I looked at the briefing documents associated with those filings (Pfizer's here and Moderna's here).  Each contains dozens of pages with charts and data on safety and efficacy.  So let's have some fun.

Bottom Line 

In case you don't yearn for details, the bottom line is: take the vaccine!

But here's a little more info: the data indicates the vaccine is about 95% effective: you are roughly 20 times less likely to get COVID if you take the full course of either the Pfizer of Moderna vaccine versus not taking a vaccine, all else being equal.  Of about 17,000 people who got the placebo at Pfizer, 162 got COVID, while of the 17,000 who got the vaccine, 8 got COVID.  For Moderna, of 14,000 who got the placebo, 185 got COVID, while of the 14,000 who got the vaccine, 11 got COVID.

Also, the side effects were carefully studied across the more than 30,000 people who received the vaccines and they are not worth mentioning except that they are normal side effects of vaccines.

[Statistical note: the strength of an effect of a treatment is often measured in terms of odds ratios.  The odds ratio for the control versus the vaccine is calculated as follows.  The numerator is the chance of getting COVID with the control divided by the chance of not getting with control.  The denominator is the chance of getting COVID with the vaccine divided by the chance of not getting with the vaccine.  Because the number of people getting COVID, whether given the vaccine or not, is huge and about the same in the treated and control group, the denominator can be ignored here.  However, in case you are interested, lets calculate the simple ratio of 185 with COVID and control divided by 11 with COVID and the vaccine (both for Moderna), which is 16.8.  Now let's compare that to the exact odds ratio, which is (185/13698)/(11/13923), which is 16.9.  Note that the 13,698 represents the people who got the placebo but did not get COVID and the 13,923 represents the people who got the vaccine but did not get COVID.  Also note here that I am flipping the ratio for ease of discussion, and rounding to 20 to 1: we would usually say the ratio is 1:16.9 because we are comparing the treatment (1) to the control (16.9). ]

How about older people?

The vaccine is clearly effective for older people (defined in these studies as >65).  What is not clear is whether it is less effective for older people than it is for younger people.  Pfizer's filing has information regarding T-cell and antibody responses, collected in Phases I and II (with about 400 participants total), and almost everyone appears to develop antibodies and a T-cell response, but older people develop fewer antibodies on average.  Of course, the real question is whether they still develop sufficient equivalent antibody protection for the purposes of stopping the disease.  Imagine that we are trying to fill a 2-gallon jug.  One person brings 10 gallons of water and the other brings 5.  Either one can fill the jug quite easily.  Not so if one brings 2 gallons and the other brings 1 gallon.

So what we really care about is whether the antibodies are sufficient to fill our water jugs: do older people develop enough antibodies from the vaccine so that they are just as unlikely to get COVID with the vaccine as younger people?  

The numbers behind the simpler question of whether the vaccine is effective at all in older people, are quite clear.  Pfizer's study had around 8,000 >65 year-olds, evenly split between treatment and control, and just 1 of the 21 people in this age group who got COVID were among the half who received the vaccine (the ratio is still about 20 to 1 treatment to control).  For Moderna, 4 received the vaccine out of 33 65+ who got COVID (the ratio is 8 to 1).  So are either of these different than the overall effectiveness of 17 to one, once we take random variation into account?

So keep in mind that below we are not testing whether it is effective in older people, but instead, we are testing whether there is enough data to say one way or the other if the vaccine is *less* effective in older people than it is in younger people.  We want to know whether it is still around 95% effective or if maybe it is a little lower.  

We can check this using a statistical test called a Fisher Exact test.  The nice thing about this is that we can completely ignore all people who did not get COVID and just zero in on those who did.  Those numbers, for Moderna, are summarized in this table.

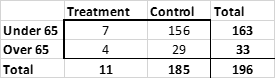
 To see if the Over 65 group is different, the Fisher Exact test takes the totals as given: we have 196 people who got COVID, and 11/196 (about 6%) among those got the treatment (vaccine).  If age does not matter, about 6% in the over 65 and 6% in the under 65 group would be part of the treatment group.  The Fisher Exact test checks the chances you would have as many as 4 out of 33 (12%) in the over 65 group that had gotten treatment given the overall total of 6%, if the differences were due to chance alone.  This is done using a Hypergeometric distribution.  I won't give further details except that the command in the R language is phyper(7,163,33,11) or phyper(7,11,185,163).  The result is that the difference is not quite statistically significant--the difference between the groups is small enough to have occurred simply by chance variation.  However, it is close, and given the lower antibodies produced by older people, it looks like the vaccine, though very effective in older people, is not quite as effective as it is in younger people.  This is just an indication and the formal statistics say wait and see if you are interested in comparing effectiveness by age.  For the Pfizer data, where there are fewer over 65, there is not even a weak indication, as the percentages are almost exactly the same.

Net-net: the vaccine works very well with older people, but perhaps not quite as well as the 95% effectiveness we are finding in younger people.  We'll need more data to know for sure.

How about severe cases?

Here the data is also unclear.  The vaccine appears to work well for severe cases also, but it is not clear if it works as well, or if maybe it works even better than it does for mild cases.  For Pfizer, despite some mumblings to the contrary in the popular press, there were only 4 severe cases in the primary study group (people who got both doses of either vaccine or placebo and were infected more than 7 days after the doses), and 3 were in the control group.  That means on a raw basis, you are roughly 3 times less likely to get severe COVID with the vaccine, effective but not as effective as the vaccine in general.  

For Moderna, the results are stronger: there were 30 severe cases in the control group but 0 in the treated group.  In other words, from the raw data, the vaccine seems to be even better at stopping severe cases than mild cases (30 times as effective).

Beyond the difference in effectiveness regarding severe cases between the Moderna and Pfizer vaccine, it is also interesting to note that the Moderna data had about 1/6th severe cases versus only about 1/50 severe in the Pfizer data.  Since this difference is mostly among the control group, it is not due to a difference in vaccines but either due to how severe cases are defined or the demographics of the test subjects and where the outbreaks were that affected them.

But is the effectiveness for stopping severe cases statistically different from the baseline, though, or could all this be noise?  We can use the Fisher Exact again.  

For Pfizer, the difference is not statistically significant, but directionally indicates that the vaccine is less effective at preventing severe cases than it is at preventing non-severe cases.  Still , the statistics say it could have just been bad luck and it's only a single case among the treated group and only 4 severe cases in total.

For Moderna, the difference is also not statistically significant, but its indication is in the other direction, indicating that the vaccine might be even better at helping to prevent severe cases.  With Moderna, there are 30 cases in total.  Of course, since the vaccine overall is 95% effective, it is not surprising that none of the 30 were among severe cases even if the vaccine were no more effective at preventing severe COVID than preventing COVID.

Net-net, there is very little data thus far regarding severe cases, but the statistics and data indicate that the vaccine is helpful in preventing severe cases.  There is not yet enough data to know whether the vaccine has more, less, or the same effectiveness against severe COVID (relative to a placebo) than its 95% effectiveness at preventing COVID in general.